The Sleeping Beauty Paradox
Written By: Vidya Sinha
The Sleeping Beauty paradox is a seemingly mundane scenario involving a sleep experiment and an oblivious girl. At first blush it may seem trivial, but further contemplation reveals several layers to the problem. In this article, let’s explore the Sleeping Beauty paradox with an analytical lens and dispel the confusion. From this point onward, I’m going to refer to it as the Sleeping Beauty problem, to dismantle the air of mystique associated with the word “paradox.”
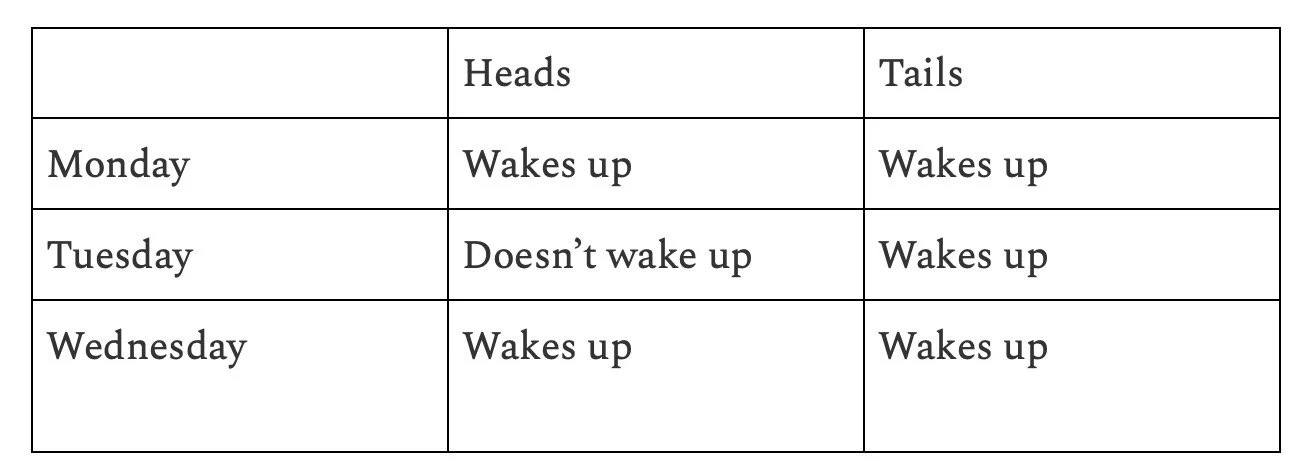
The situation is as follows: Sleeping Beauty participates in a sleep experiment in which she is initially given a sleeping pill on Sunday. She is given all the information about the experimental setup. Then, the experimenters toss a fair coin. If it comes up as “heads,” Sleeping Beauty is awakened on Monday, after which she is given another sleeping pill. However, if it comes up as “tails,” Sleeping Beauty is awakened on Monday, given another sleeping pill as before, but then additionally awakened on Tuesday. Finally, regardless of the outcome of the coin, Sleeping Beauty is awakened on Wednesday. Every time she wakes up, the experimenters ask her the following question: what is the probability that the coin displays “heads”? Alice has no knowledge of what day it is every time she wakes up and has no memory of waking up previously.
One common answer is ½, as the coin is fair, so shouldn’t the probability of receiving “heads” simply equal ½? If you’ve read our Monty Hall Problem article, you will be wary of this line of reasoning. This logic misses the crucial fact that if the coin came up heads, she wakes up less frequently overall than if it came up tails, meaning that if she wakes up, she should assign a slightly higher probability to the original coin toss being “tails.” With this in mind, let’s try to calculate the probability.
With this table, we can calculate the probability by considering each day separately. For each day, there is a ⅓ probability that it is that day.
The probability that the coin comes up heads if she wakes up on Monday is ½.
The probability that the coin comes up heads if she wakes up on Tuesday is 0.
The probability that the coin comes up heads if she wakes up on Wednesday is ½.
Altogether, the probability that it is heads is ⅓(½ + 0 + ½) = ⅓. Let’s sanity check this: it aligns with our initial hunch that the probability that the initial toss was tails should be slightly higher, and ⅔ is indeed larger than ⅓. Now that we’ve solved the problem- what’s all the buzz about?
In reality, the Sleeping Beauty problem is quite controversial, with a sizable number of people believing the answer is ½. The reasoning for this is that the event of waking up bears no new information since Sleeping Beauty is already privy to the experimental setup. Therefore, the probability of the coin-toss being “heads” should not change from the prior probability of ½. After all, waking up entails exactly the same experience regardless of the coin toss.
One common rebuttal to this line of reasoning is the argument of extremes. If instead of merely being awakened one additional time in the event of the coin coming up as “tails,” Sleeping Beauty is instead woken up every day forever, what is the probability of the coin being “heads?” Intuitively, it is almost certain that the coin came up tails, making the ½ probability nonsensical. Or even more extreme: what if she is never woken up in the case of the coin coming up as “heads?” Then, if she does wake up, there is a probability of 0 that the coin came up heads. These extreme hypotheticals effectively refute the notion that the event of waking up should not influence the probability estimate.
Conclusion
It’s important to acknowledge that the ⅓ probability does not contradict the coin’s fairness. The overall probability that the coin will be heads in an arbitrary future toss remains ½. However, the problem fundamentally asks for the probability of what the coin toss was, and the contrasting outcomes of heads and tails are what produce the answer of ⅓.
Confusion is a product of the mind, not a feature of reality. There are no true paradoxes, there are only tough problems!
Works Cited
Bischoff, M. (2024, February 20). Why the “Sleeping Beauty Problem” Is Keeping Mathematicians Awake. Scientific American. https://www.scientificamerican.com/article/why-the-sleeping-beauty-problem-is-keeping-mathematicians-awake/