The Shoelace Theorem

Written by: Ritvik Ranjan

In the world of mathematics, there exists many, many different theorems. The names of these theorems are typically chosen by their discoverers. Some of these names are representative of the ideas themselves, or their founders. However, some theorems have completely unique and unexpected names not traditionally associated with mathematics. In this series of articles by Science Rewired, we explore the weirdest-named math theorems out there, as well as what they do and how they work.

The Shoelace Theorem, despite its laughable name, is very useful in geometric mathematics. Proposed by the mathematician Albrecht Meister, this theorem became a foundation of many higher uses for polygon geometry.

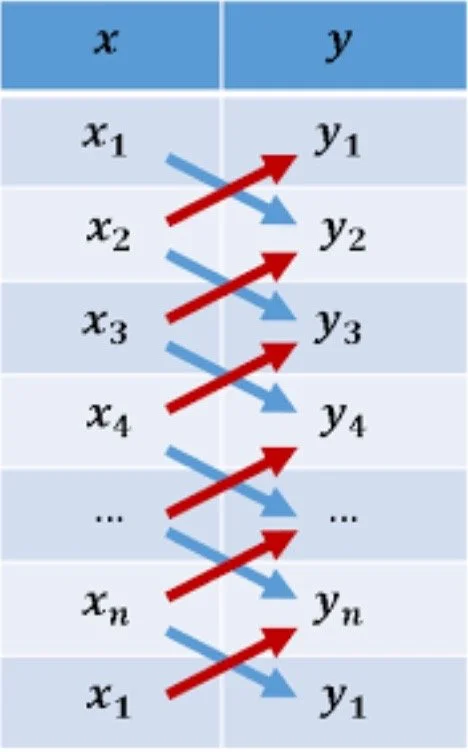
The Shoelace Theorem offers a method for calculating the area of a polygon given the coordinates of its vertices. The theorem derives its name from the systematic "crisscrossing" pattern similar to lacing up a shoe, employed in the calculation process. By arranging the vertices

of a polygon in a sequential order and computing a specific summation involving these coordinates, the theorem yields the polygon's area. Remarkably, this method applies regardless of the polygon's complexity or the number of its sides, making it a versatile and indispensable tool in computational geometry.

Mathematically, the Shoelace Theorem is defined as such: If the polygon P has vertices (x_1, y_1), (x_2, y_2), ... , (x_n, y_n), listed in clockwise order, then the area (A) of P is:

This seemingly convoluted formula is truly quite basic. The minus sign within the absolute value bars represents the "crisscrossing" summation, while the multiplication by 1/2 ensures the proper

computation of the polygon's area. The variables simply represent the coordinates of the polygon’s points.

Beyond its primary application in polygonal geometry, the Shoelace Theorem finds utility in diverse fields ranging from computer graphics and image processing to geographic information systems. Its simplicity, efficiency, and accuracy make it indispensable in scenarios that need rapid and precise area computations.

In conclusion, while the Shoelace Theorem may sport an unconventional name within the field of mathematics, its significance and utility remain undeniably profound. From its humble origins in polygonal geometry to its adoption across various other fields, this theorem shows the ingenuity and versatility present in the mathematical world. As we traverse the vast landscape of mathematical theorems, the Shoelace Theorem serves as a poignant reminder of the boundless creativity and unexpected inspirations that shape the realm of mathematics.

Works Cited:

Art of Problem Solving. (n.d.). https://artofproblemsolving.com/wiki/index.php/Shoelace_Theorem

A., & A. (2023, March 5). The Shoelace Algorithm - 101 Computing. 101 Computing - Boost Your Programming Skills! https://www.101computing.net/the-shoelace-algorithm/

Area of a Triangle | Brilliant Math & Science Wiki. (n.d.). https://brilliant.org/wiki/triangles-%20calculating-area/

Wikiwand - Shoelace formula. (n.d.). Wikiwand. https://www.wikiwand.com/en/Shoelace_algorithm