The Uncertainty Principle Debunked

Written by: Aadarsh Srinivasan

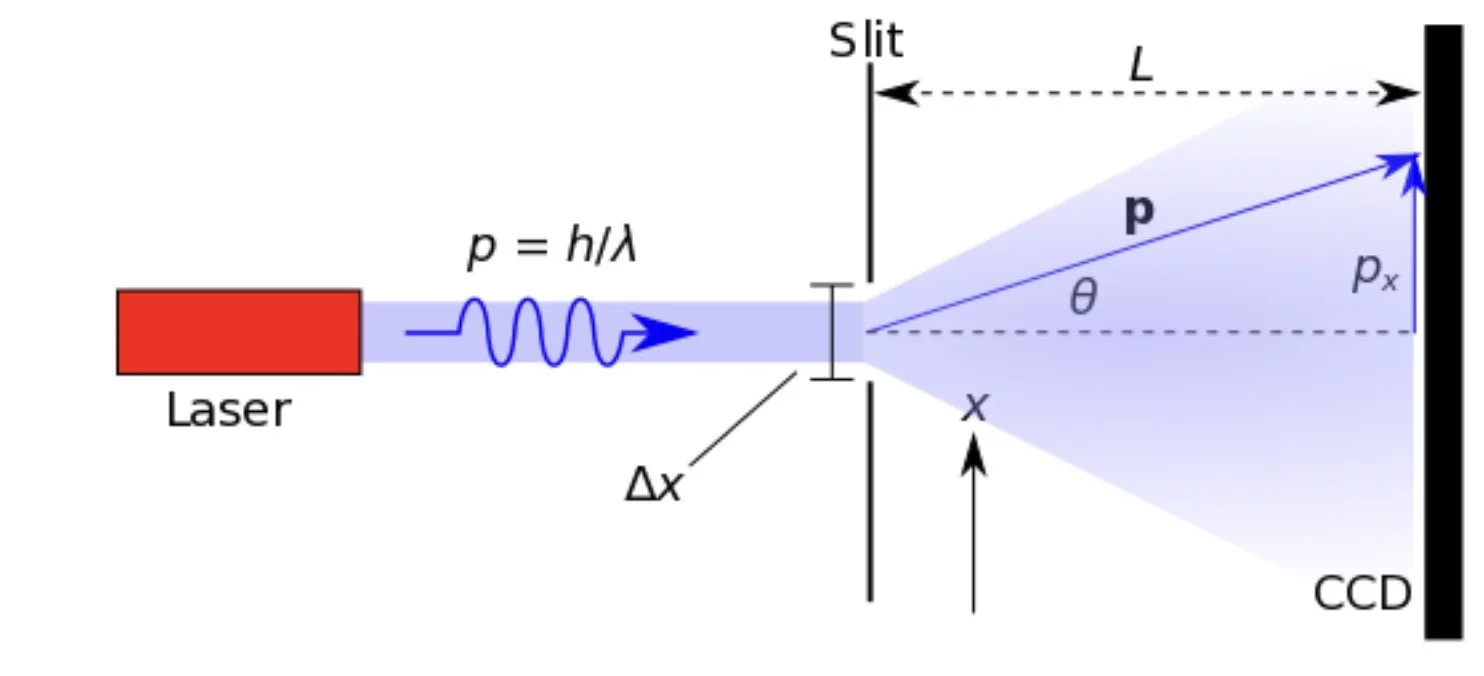
Imagine that you shine a laser through a slit. The narrower you make the slit, the narrower the light gets. However, at a certain point, eventually, the light counterintuitively starts getting wider and wider, even though the slit is getting narrower. But why does this happen? This article from Science Rewired will delve into the phenomenon of the uncertainty principle and why it happens.

Werner Heisenberg was a German physicist who made many contributions to the field of quantum physics. For this particular experiment, he attempted to measure the position and the momentum of a particle simultaneously, but he keeps getting uncertainties regarding both the particle’s location and momentum.

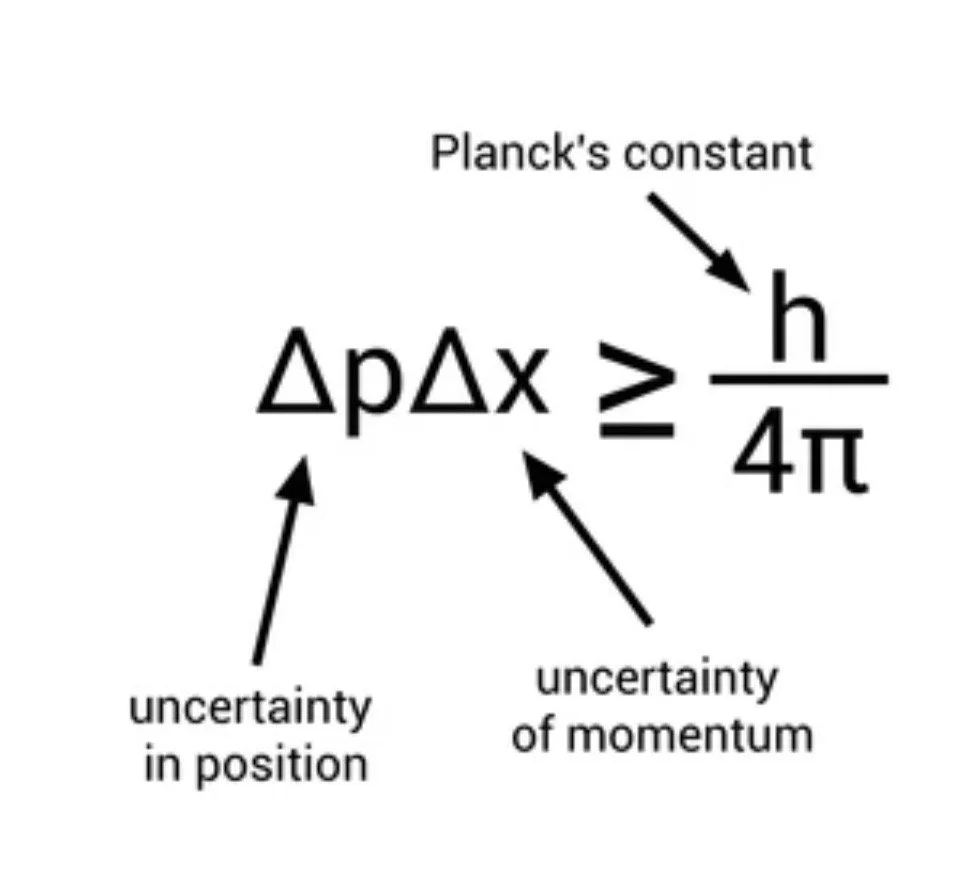
The Heisenberg Uncertainty Principle states that you cannot know both the position and momentum of a particle with perfect accuracy. The formula states that the uncertainty of the position multiplied by the uncertainty of momentum is greater than or equal to Planck's constant divided by 4π.

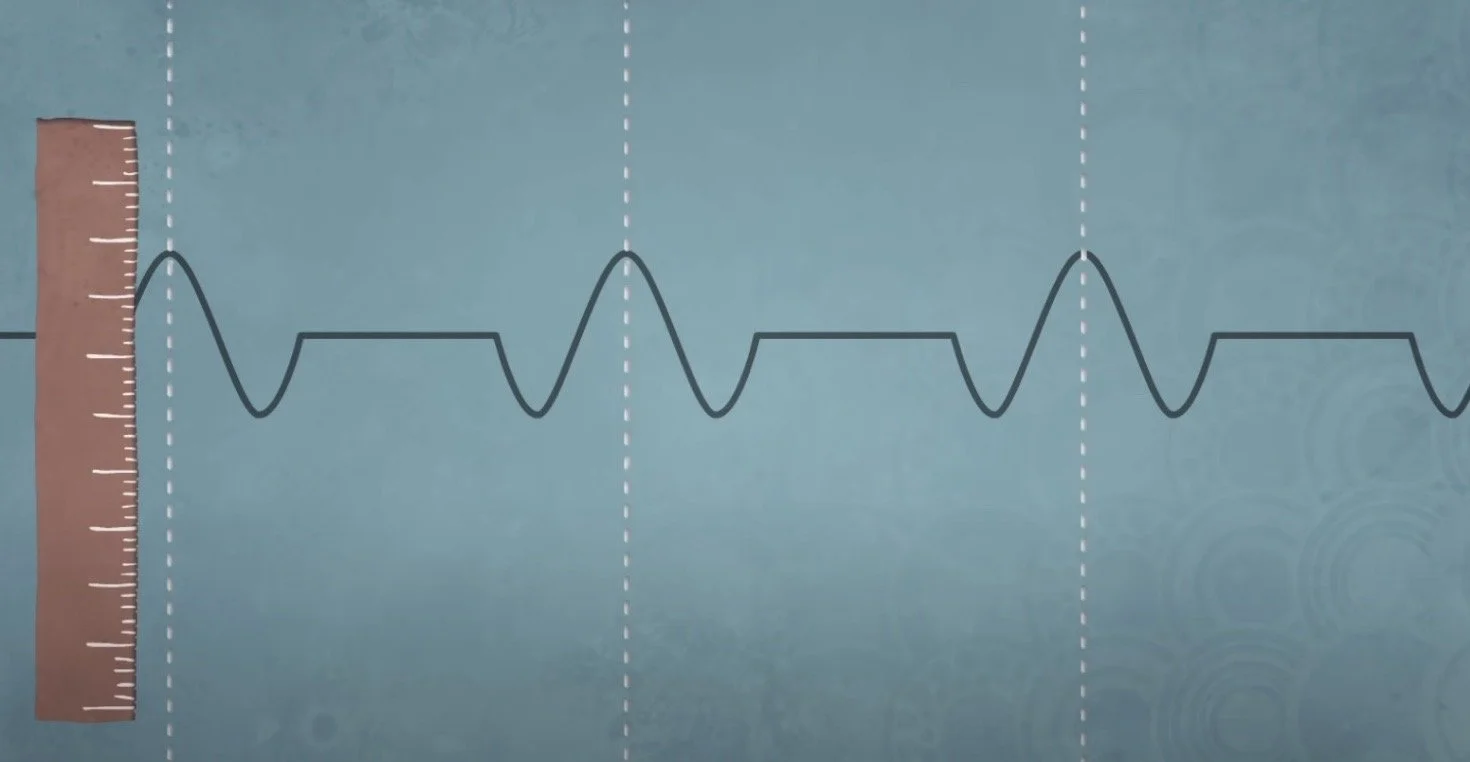
Now, this concept is a little counterintuitive; you can’t know the particle’s exact position and momentum. After all, in our empirical world, you would know that you are going 45mph (the speed limit for example), and you would know exactly where you are driving. However, it is important to remember that in quantum mechanics, it is denoted that all matter behaves as both a particle and a wave. An object’s wavelength is related to its momentum. A higher momentum causes a lower wavelength. For example, a hippo would have a very very very short wavelength, as it has a high momentum. However, some particles would have wavelengths that could be measured in experiments, and thus, a really low momentum.

If we have a wave, we will know its momentum. However, the wave then won’t have a definite position. And if we study a particle, we can know its definite position, but then we won’t have be able to derive any information regarding its momentum. But how do we find both? We need an area with waves in a small area, and we can find that by combining waves. The more waves that are combined, the more the wave amplitudes cancel out, and we can find the amplitude of the wave in that particular area.

Therefore, we have found a wave section in a section in space, but to do so, we had to sacrifice certainty in both position and momentum, which can be related back to the formula at the top. This proves that we cannot know the exact position and momentum of an object, which proves Heisenberg’s Uncertainty Principle.

So remember this, the next time you are caught speeding, and the police officer tells you that you were traveling at 90 miles per hour, just say, “Drat, now I don’t know where I am!”