Non-Euclidian Geometry

Written By: Ritvik Ranjan

Through past interactions and experiences, I have come to the assumption that non-Euclidean geometry is a topic that often comes up as being “nerdy” or “boring”, but no one really knows what it is. So, I decided that it would be a topic that would be interesting to learn more about. As I researched, I was blown away by the fact that we students haven’t even breached the surface of all geometry. Join this exploration of non-Euclidean Geometry on Science Rewired to put the field of geometry into perspective.

Imagine you're used to drawing lines and shapes on a flat piece of paper—this is what's called Euclidean geometry, named after the ancient Greek mathematician Euclid. In Euclidean geometry, you're probably familiar with concepts like parallel lines never meeting and the sum of angles in a triangle equaling 180 degrees.

Now, in non-Euclidean geometry, things change when you explore spaces that don't adhere to these "flat" rules. There are mainly two types of non-Euclidean geometries: spherical and hyperbolic.

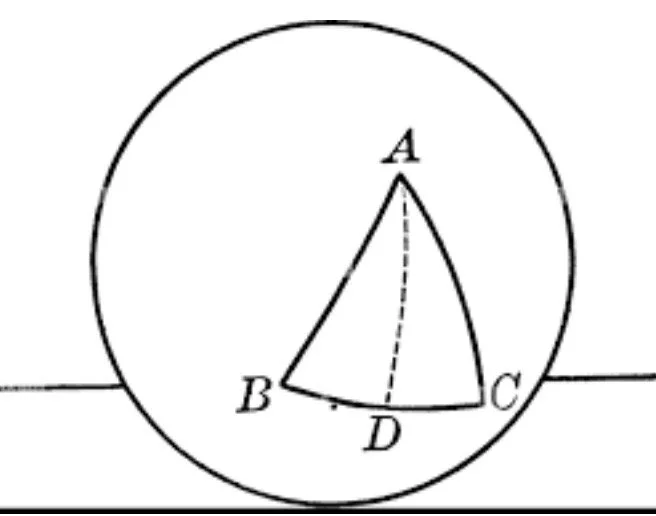
Spherical Geometry: Think about the surface of a sphere, like the Earth. Lines on the surface of a sphere aren't straight like the lines on a flat paper. They curve around the sphere. In this geometry, if you draw two lines (think of them as great circles) that start out as parallel at the equator and extend towards the poles, they will intersect at the poles. So, in spherical geometry, lines that seem parallel eventually meet. Additionally, when you draw a triangle on the surface of a sphere, every side of the triangle follows a curved path along the sphere's surface. As a result, the angles formed by these sides get "compressed" or "bent inward" due to the curvature of the sphere. This compression effect causes the sum of the angles in a triangle to exceed 180 degrees, diverging from the familiar 180-degree sum found in Euclidean geometry on flat surfaces.

A right triangle on a spherical object

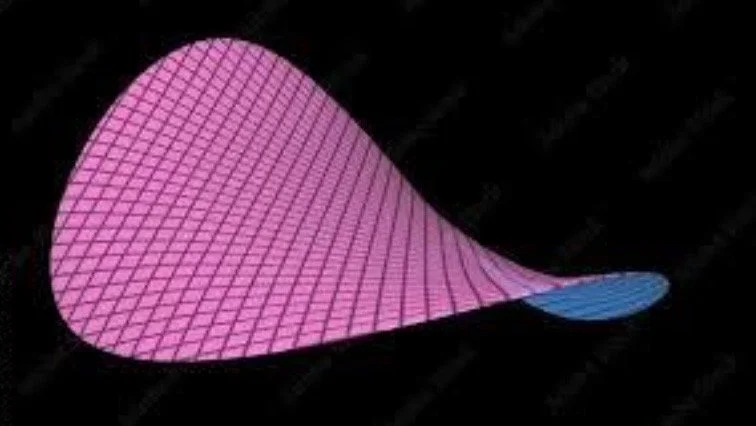
Hyperbolic Geometry: Here, things get a bit different. Imagine shapes on a surface that curves away from itself. In hyperbolic geometry, lines diverge more quickly than they would in flat space. If you draw two parallel lines in hyperbolic geometry, they will actually diverge away

from each other continuously. Additionally, the angles on a triangle do not equal 180 degrees in hyperbolic geometry, similarly to spherical geometry. However, in hyperbolic geometry the angles on a triangle equal fewer than 180 degrees, as it is curved outward and the side is “stretched out”, causing the angles to be smaller.

A Hyperbolic Paraboloid

These non-Euclidean geometries challenge the assumptions made in Euclidean geometry about parallel lines, angles, and the overall shape of space. They help us understand that there can be different ways to define space and geometry beyond what we might consider as "normal" or flat.