The Not-So Mysterious World of Neural Networks-
Written By: Vidya Sinha
Science in the 21st century has seen a crucial paradigm shift following the advent of machine learning techniques. By taking advantage of computational power and mathematical algorithms, machine learning provides a robust toolkit with which to tackle complex problems. This toolkit enables researchers to make accurate predictions about the world using enormous amounts of data that would otherwise evade analysis, proving invaluable in a diverse selection of fields- from market forecasting, to autonomous vehicles, to cellular biology.
As a rapidly burgeoning field, machine learning has infiltrated chat forums, institutions, and social networks with its jargon. To appreciate the vast potential of the field, it is necessary to understand these underlying concepts. In this article, we’ll dip our toes into the field with the concept of a neural network.
Classification and Regression
Before we delve into the details of a neural network, we must understand the central theme of machine learning. Abstractly speaking, machine learning seeks to map a set of inputs, or “features,” to one or more outputs. Usually, these “features” correspond to the attributes of some real-world entity, such as the health profile of a patient or the Olympic track record of an athlete. Machine learning provides a set of algorithms for manipulating this initial information to arrive at a statistically plausible prediction about the original entity. In our patient example, this could entail finding the probability that a patient develops cancer as a function of their existing health profile. Machine learning is about generating that function so that we can use this function to predict if an arbitrary patient will develop cancer.
There are two domains of prediction, different in principle but similar in practice. One is regression, in which the output is a numerical value, such as the salary of a person in ten years or the percentage of yellow pigment in a flower. In mathematical terms, this is equivalent to mapping a feature vector to a scalar output.
The other is classification, which uses the values supplied by regression to determine the categorical placement of the entity. Here, the output is if a person is a successful businessman or not, or if it is a sunflower or a rose. The mathematics behind these two processes is very similar, although classification requires the addition of a function that determines the category of the entity in question. The difference between regression and classification is the difference between remarking, “oh, that animal has an awfully long neck!” and proclaiming, “oh, that animal is a giraffe!”
Why Neural Networks?
Linear classification functions by taking a weighted sum of the feature inputs to determine the output. It is initially given a dataset of entities (feature vectors) and their respective outputs (the feature we are evaluating) and based on this information, it creates weights that will maximize the likelihood of the original dataset.
Essentially, the algorithm devises a specific weighted sum to predict outcomes based on inputs, using sample inputs and outputs to assign the most reasonable weights. The fact that it is simply a weighted sum (think linear equations, but with multiple variables) is why the term linear is attributed to the function. But what if the function that best predicts outcomes isn’t simply a weighted sum; what if it isn’t linear? This is where neural networks come into play, outshining linear regression and classification by several orders of magnitude.
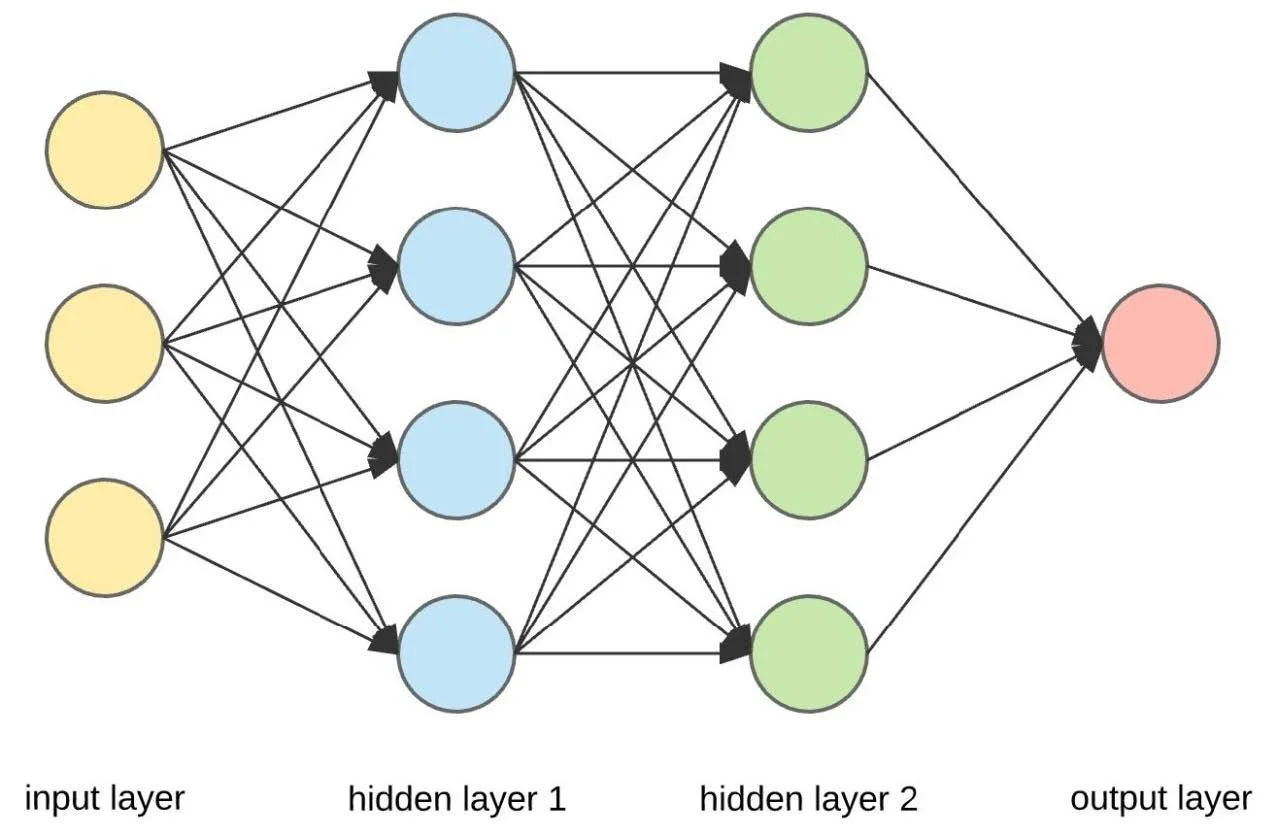
Neural Network Architecture
The neural network is composed of several layers of smaller computing units called nodes. What is the significance of these layers? Initially, the nodes of the first layer are supplied with a set of parameters corresponding to the original entity’s features. Then, the neural network takes a weighted sum of these features and sends this to every neuron in the next layer of the network. The weights of these weighted sums are specific to every pair of neurons exchanging information. These weights are mathematically determined using the algorithm of backpropagation, which works in tandem with multivariable calculus to align the neural network with training data by working backwards from outputs to inputs.
(Stay with me, intrepid readers! If you’ve gotten this far, you can make it to the end of the article.)
Now we arrive at the non-linear portion. When each of the nodes receive their node-specific weighted sums, this sum is then inserted into a nonlinear function to generate the value of the node that will be relayed to the next layer of the network. This is called the activation function. The most common activation function is ReLU, which converts the weighted sum into a number from 0 to 1. The neural network is essentially composed of many such mini-regressions, making for a multilayered and dynamic calculation. More concretely, every layer of the network essentially draws a conclusion about a trait of the individual entity, and the entire neural network leverages each of these individual conclusions to come to an overall classification decision. This is fundamentally different from simply taking a single weighted sum of the original attributes given. It is the difference between taking a person’s resume and directly predicting their career success, and taking their resume, using it to predict their social skills, street smarts, and quantitative intelligence, and then using these conclusions to predict their career success.
At the end of the neural network, the final outputs will be stored in the last layer, and whatever neuron has the largest value will generally indicate the classification information of the entity whose features were initially inserted. Nifty!
The mathematics of neural networks draw heavily from multivariable calculus and statistics. By realizing that any regression or classification model must maximize the probability of a given dataset and that we desire to minimize the deviation of our model’s predictions from the actual given values, we can appreciate why statistics and calculus are such invaluable tools for machine learning; statistics deals with these crucial probabilities, and calculus deals with minimizing errors. In machine learning, these two fields synergize to create an infinitely powerful algorithmic framework for problem solving.
This article only scratches the surface of the rich world of machine learning. I encourage inquisitive readers to scour the web for further information, as there is no shortage of educational videos and articles explaining machine learning concepts.
As always, stay curious.
Works Cited
What are Neural Networks? | IBM. (n.d.).
https://www.ibm.com/topics/neural-networks
Brempong, K. A. (2021, December 15). I Finally Understood Backpropagation: And you can too. . .. Medium. https://towardsdatascience.com/i-finally-understood-backpropagation-and-you-can-too-44f7dd98ff52#:~:text=The%20backpropagation%20algorithm%20is%20one,understanding%20how%20things%20really%20
Roy, A. (2021, December 14). An introduction to gradient descent and backpropagation. Medium. https://towardsdatascience.com/an-introduction-to-gradient-descent-and-backpropagation-81648bdb19b2