P-Adic Numbers

Written By: Aadarsh Srinivasan

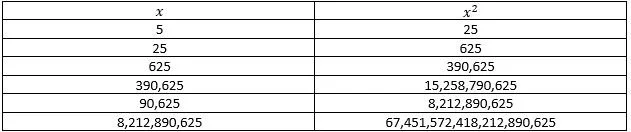
Take the number 5. Square it, and you get 25. Take the number 25. Square it, and you get 625. Take the number 625. Square it, and you get 390,625. There is a pattern. 5 squared ends in 5. 25 squared ends in 25. 625 squared ends in 625. Now, 390,625 squared doesn’t end with 390,625 (it results in 152587890625), but it does end with 90,625, so let's square that.

These numbers are converging onto a single value, but this number doesn’t approach a specific value. This value approaches infinity. So this number has infinite digits to the left of the decimal point, instead of the right. These numbers are called p-adic numbers, and they have an infinite number of digits to the right of the decimal point (p is the number of possible values for each digit starting from 0). But what are these numbers used for, and why are they practical?

The 10-adic numbers are numbers with an infinite amount of digits that are 0-9 (10 possible digits which is why they are called 10-adic) to the left of the decimal. An example of a 10-adic number would be …182359832581539635035. This number ends with 182359832581539635035 and has infinite digits to the left of the decimal (which is implied as .0). Each value in the p-adic number set is equivalent to a value in the real number set.

You can add and subtract p-adic numbers with no problems:

So what would the 10-adic number …666666668 be equivalent to? Well 4/3 of course! You can multiply with p-adic numbers too. How is that possible though? Well, when we multiply and infinite number of 6s ending with an 8 with a 3, we get a 4 in the 1’s place, and then 0’s forever to the left.

... 666666668

× 3

______________________

... 000000004

When you multiply 8 by 3, you get 24, so you write a 4 and the 2 gets carried over. 6 times 3 is 18, and you add 2, which gives you 20, and you write a 0, and the 2 gets carried over. 6 times 3, again, is 18 and when you add 2, you get 20, you write 0, and the 2 gets carried over again. This goes on infinitely left, and there are only 0s after the 4. It may seem like there must be a 2 at the end, but there can’t be because the 6s go on forever too, and there is no place to fit in the 2 at the end. Now that we know that …666666668 x 3 = 4, we can divide both sides by 3, and we get the counterintuitive statement that …666666668 = 4/3.

Using p-adic numbers, we can represent fractions and positive numbers, but what about negative numbers? Well, p-adic numbers can represent those too!

... 999999999

+ 1

______________________

... 000000000

If you take the 10-adic number …999999999, and add 1 to it, you get an infinite number of 0’s to the left, which is equal to 0. By that logic, if …999999999 + 1 = ...000000000, then if you subtract 1 from both sides, you get …999999999 = …000000000 - 1 which means …999999999 = -1. Using this method, we can conclude that p-adic numbers can represent positive numbers, negative numbers, and fractions, all without a decimal point.

The versatility of these numbers are very useful in the field of mathematics, like in number theory, algebra, and problem solving. Mathematicians study these numbers with great interest, as they are very fun and useful to use in the modern world of mathematics.