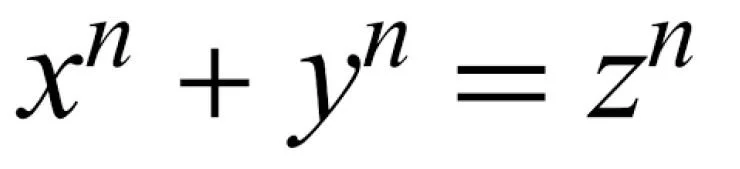The Quest for Fermat's Last Theorem: Andrew Wiles' Peregrination
Written By: Ritvik Ranjan
The story of how Andrew Wiles discovered the proof for Fermat's Last Theorem is nothing short of a mathematical odyssey, filled with passion, perseverance, and an unwavering commitment to unravel one of the most enduring mysteries in mathematics.
Fermat's Last Theorem, a tantalizing conjecture posed by the French mathematician Pierre de Fermat in the 17th century, served as the linchpin of Wiles' mathematical journey. The theorem stated that no three positive integers a, b, and c could satisfy the equation a^n + b^n = c^n for any integer value of n greater than 2. Despite its deceptively simple appearance, the proof of this theorem had eluded mathematicians for centuries, becoming one of the most notorious unsolved problems in the field.
Wiles' fascination with Fermat's Last Theorem began during his childhood when he stumbled upon a book that contained a reference to the theorem. Intrigued by the enigmatic statement, he embarked on a journey that would consume his life's work. Little did he know that this journey would span several decades and become the greatest mathematical challenge of his generation.
Wiles' first attempt to tackle Fermat's Last Theorem came in the form of a youthful ambition. As a 10-year-old, he boldly declared to his schoolteacher that he would one day prove the theorem. However, he soon realized the daunting nature of the task, as he encountered the deep complexities and intricacies involved in the proof.
The turning point in Wiles' quest came in 1986 when he made a fateful decision to take a sabbatical from his teaching position at Princeton University. He decided to dedicate his time to cracking Fermat's riddle. Wiles immersed himself in the world of elliptic curves and modular forms, two seemingly unrelated areas of mathematics that would ultimately hold the key to the theorem's solution.
Years of painstaking research and sleepless nights followed. Wiles faced numerous obstacles and setbacks, and at times, it seemed as though the theorem would forever elude him. Yet, his determination remained unshaken. He toiled in relative obscurity, with only a handful of trusted colleagues aware of the magnitude of his endeavor.
Then, in 1993, came the breakthrough. Wiles made a remarkable connection between elliptic curves and modular forms, a connection that had eluded mathematicians for centuries. It was this groundbreaking insight that would ultimately pave the way to the proof of Fermat's Last Theorem.
Wiles' presentation of his proof in 1994 sent shockwaves through the mathematical community. His 108-page manuscript, filled with intricate mathematics and profound insights, was met with both awe and skepticism. The scrutiny that followed was intense, as mathematicians worldwide inspected each line of his work.
In the end, Wiles' proof withstood the rigorous examination, and Fermat's Last Theorem was confirmed to be true. The mathematical world celebrated this momentous achievement, and Andrew Wiles' name became forever etched in the annals of mathematical history.
Wiles' journey to proving Fermat's Last Theorem serves as a testament to the unyielding spirit of exploration and discovery that drives mathematicians. It is a story of dedication, resilience, and the relentless pursuit of knowledge—a story that continues to inspire generations of mathematicians to dream big and tackle the most profound mathematical challenges.
Works Cited:
Singh, Simon. (1997). Fermat's Enigma: The Epic Quest to Solve the World's Greatest Mathematical Problem. Anchor Books.
Ribenboim, Paulo. (1996). Fermat's Last Theorem: For Amateurs. Springer.
Wiles, Andrew. (1995). Modular Elliptic Curves and Fermat's Last Theorem. Annals of Mathematics, 141(3), 443-551.
Andrew Wiles - Biography. Maths History. (n.d.). https://mathshistory.st-andrews.ac.uk/Biographies/Wiles/